Mathematics and Geometry

The Montessori key lessons are extensive, covering many concepts explored in High School.

The topics covered in the Primary classrooms, in line with the NSW Education Standards Authority (NESA) K-6 syllabus, include:

• Addition, subtraction, multiplication and division with whole numbers
• Fractions and decimals
• Patterns and algebra
• Data.

In line with each child’s development, the topics explored in Montessori primary classrooms which extend beyond the K-6 Syllabus include:

• Square root
• Cube root
• Squaring and cubing numbers
• Powers of numbers
• Long division
• Multiples and factors
• Foundations in algebraic equations
• Different number bases.

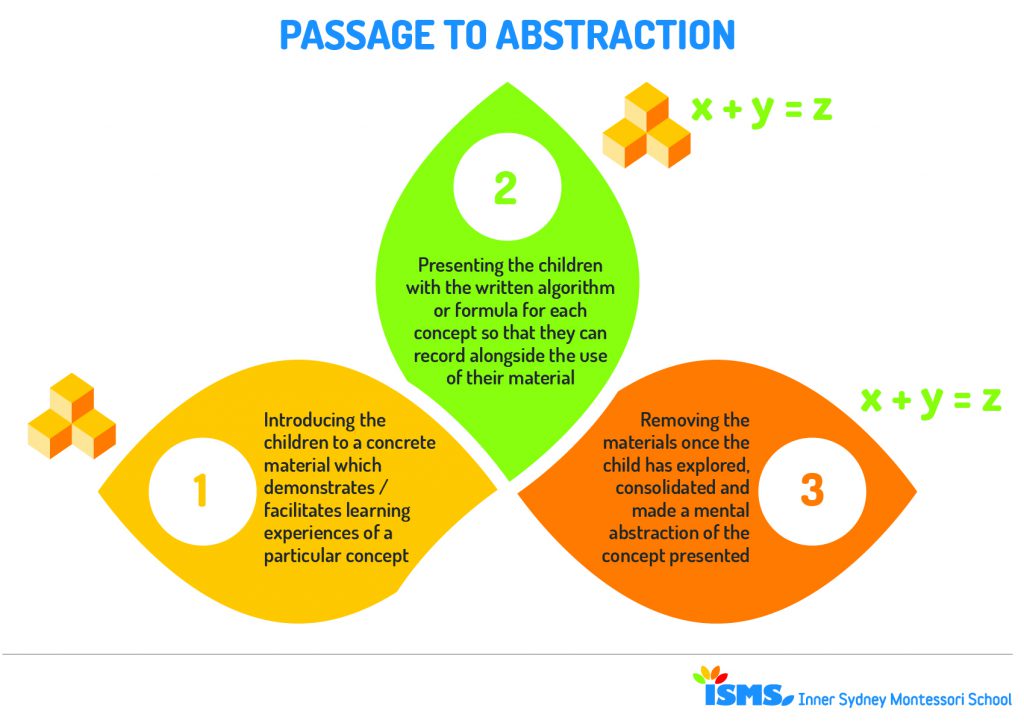
Montessori lessons in Mathematics follow what is known as the ‘passage to abstraction’. An abstraction is the mental concept, understanding or strategy that a child is eventually able to independently apply to solve a given problem, without the use of any material. The passage is the series of learning experiences that take place in the child’s mind to support the development of the abstraction.

Mathematics is seen as a tool for children to grasp the immensity and complexity of the universe we live in.

All early work in mathematics begins with concrete materials in order for the children to engage in their own activity and become autonomous learners (able to learn independently).

Each new lesson builds from a previous concept, forming a continual stream of learning which follows each child’s developmental needs. For this reason, lessons can be taught individually when needed, with many taught in pairs and small groups. Lessons are repeated as many times as needed for each child.

Many foundational concepts in mathematics are introduced to the children in the 3 – 6 (Stage 1) classroom. The materials that follow in the 6 – 9 (Stage 2) classrooms then build upon these foundations.

While materials are still greatly utilised in the 9 – 12 (Stage 3) classroom, there is a focus on supporting the children to move to abstraction of mathematical processes. Abstraction involves recording algorithms on paper, using mental mathematics and problem solving strategies. The materials:

The materials:

• follow a natural and fluid progression from the concrete experience to the mental abstract abstraction.
• generally follow the passage to abstraction. They introduce the children to a concrete material which demonstrates/facilitates learning experiences of a particular concept, present the children with the written algorithm or formula for each concept so that they can record alongside the use of their material and remove the materials once the child has explored, consolidated and made a mental abstraction of the concept presented.
• provide the opportunity for the children to explore mathematical concepts/understandings independently and make their own discoveries.

Following on from concrete materials, the children develop their own mental visualisations of mathematical concepts, built from the materials they have used. This is referred to as a materialised abstraction.

Mathematical abstractions and mental strategies are formed strongly in the child’s mind through their repetition of activity and a diversity of work with different materials.

All Areas of the NSW syllabus are covered within the Montessori Key Lessons for Geometry. These topics include:

• Measurement (length, area, volume and capacity, mass, time)
• Lines and angles
• Polygons (2D shapes)
• Solid Geometry (3D shapes)
• Position.

The Montessori Key Lessons provide children with learning experiences which extend beyond the NSW syllabus, including:

• Explorations of Pythagoras’s theorem and Euclid’s theorem
• The Study of the Circle: Pi, area, circumference
• Area and volume of more complex 2D and 3D shapes such as triangles, circles, cones, pyramids
• More in depth work with lines and angles
• Equivalence between plane and solid figures.

• Lessons are taught in pairs or small groups to allow for group collaboration.
• Lessons are presented to the children using a material to demonstrate new concepts and give inspiration for the children’s follow-up work.
• Lessons provide children with tools for experiencing, understanding and observing the physical environment around them.
• Geometry is respected for its usefulness to humans throughout history.
• Many key connections are made between Geometry, History and Biology.
• Geometry is strongly linked to art and artistic design.

• The children are encouraged to use and manipulate concrete materials to develop their own understanding through exploration.
• Concrete materials are used to provide children with a hands-on experience of the formulas utilised in geometry. This not only allows children to discover how a formula is applied but also why these relationships are applicable and consistent.
• Many lessons are introduced through the telling of a story to highlight to the children the purpose and relevance of the concept being taught.